Eh, ma i tedeschi hanno investito!
Voi l'avete mai sentito un piddino, uno di quelli puri e duri, di quelli che invocano la Wehrmacht, di quelli che farebbero rastrellamenti e decimazioni in tutti i ministeri (tranne quello dove lavorano loro), di quelli che chiuderebbero tutti gli ospedali (tranne quello del loro borgo), di quelli che "Berlusconi è un porco" (ma poi si scopano la vicina del piano di sopra), ecc. (ognuno di voi potrà proseguire questa enumerazione, questo deve essere un post corto)?
L'avete mai sentito?
Fra le tante scemenze che il piddino ci somministra, la più colossale è questa: "Eh, ma i tedeschi sono competitivi perché hanno investito!".
Ah sì? Tu da questo già capisci l'asino, perché il fatto è che siccome nihil ex nihilo, se uno è un esportatore netto, è quasi matematico che avrà investito troppo poco.
Ricordo brevemente perché (è più facile dei logaritmi, tranquilli). Il punto è semplice e deriva dall'uguaglianza fra offerta e domanda. L'offerta aggregata (il Pil) di un paese è Y, e il suo valore coincide con quello dei redditi distribuiti e quindi percepiti. La domanda, cioè la spesa (perché in macroeconomia la domanda non è un desiderio ma un acquisto) è la somma dei consumi delle famiglie, di quelli dello stato, delle spese per investimento degli imprenditori, delle spese che i non residenti fanno nel nostro paese (le nostre esportazioni), alle quali sottraiamo le importazioni, perché sono spese che noi facciamo in altri paesi, e quindi generano reddito in quei paesi, e non nel nostro.
Da qui deriva l'ovvia relazione:
Y = C + G + I + X - M
che si legge: il Pil è uguale alla somma della spesa per consumi (privati e pubblici), investimenti e esportazioni, meno le importazioni.
Bene: ora voi vi ricordate che se porto una cosa dall'altra parte dell'uguale il segno cambia, no? Non mi fate come Uga, vero (che ancora non deve effettuare questo doloroso passaggio, ma io già me lo pregusto: Vorfreude ist die schoenste Freude...).
Ecco, allora portiamo un po' di cosette a sinistra (operazione di questi tempi piuttosto difficile):
Y - C - G - I = X - M
Ora, ricordiamoci di una cosa molto semplice: cos'è il risparmio? Quello che si guadagna, meno quello che si consuma. Succede a noi singolarmente, e ci succede anche collettivamente. In altri termini, in contabilità nazionale il risparmio nazionale è S = Y - C - G. Se sostituiamo questa definizione, abbiamo la formuletta magica che fa capire tante cose:
S - I = X - M
ovvero: lo scarto fra risparmio nazionale e investimento nazionale (il risparmio "netto" di un paese) corrisponde allo scarto fra esportazioni e importazioni (le esportazioni "nette" di un paese, cioè il suo saldo commerciale).
Ne consegue che se in un paese X-M ha un valore abnorme, come accade in Germania con grande gioia di tutti, americani compresi, necessariamente dall'altra parte o il risparmio è altissimo (ma questo significa che il consumi devono essere rasoterra), o, se i consumi sono fisiologici (e quindi è tale anche il risparmio) dovranno essere bassini gli investimenti. Non si scappa: non è nemmeno matematica (che potrebbe essere un'opinione, come i miei amici matematici esperti di congetture sanno): è aritmetica, esiccome i numeri naturali pare li abbia creati Dio, credo che da essi sia più difficile sfuggire che dalla morte.
Infatti:
Qui avete la media sul periodo 1999-2007 (dall'entrata nell'euro allo scoppio della crisi) del rapporto fra investimenti fissi lordi e Pil). Le fonti sono il WEO per gli investimenti totali e AMECO per quelli in fabbricati residenziali (dwellings). Ora, se ci fate caso, la Germania si piazza ultima come rapporto investimenti/Pil sia in termini totali (l'intera barra) sia escludendo gli investimenti residenziali (cioè considerando la sola barra blu). Pensate che in termini di investimenti non residenziali riesce ad essere, se pure di un pelo, sotto alla Grecia. I due paesi con il maggior livello di investimenti non residenziali sono Austria e Portogallo (guarda te)! E, comunque, anche in questa classifica, come in quella della spesapubblicaimproduttiva, stanno peggio dell'Italia solo paesi virtuosi: la Finlandia, l'Olanda, la Francia e la Germania...
Ma non è che c'è qualcosa della virtù che ci sfugge? A noi non so, ai piddini di sicuro.
E la morale della favola qual è? Che da che mondo è mondo, nella maggior parte dei casi non si diventa competitivi "investendo", ma in un modo molto più semplice e che alle élite tedesche viene tanto naturale (come ricorda l'imprescindibile libro di Vladimiro): fottendo il prossimo.
Amen.
L'avete mai sentito?
Fra le tante scemenze che il piddino ci somministra, la più colossale è questa: "Eh, ma i tedeschi sono competitivi perché hanno investito!".
Ah sì? Tu da questo già capisci l'asino, perché il fatto è che siccome nihil ex nihilo, se uno è un esportatore netto, è quasi matematico che avrà investito troppo poco.
Ricordo brevemente perché (è più facile dei logaritmi, tranquilli). Il punto è semplice e deriva dall'uguaglianza fra offerta e domanda. L'offerta aggregata (il Pil) di un paese è Y, e il suo valore coincide con quello dei redditi distribuiti e quindi percepiti. La domanda, cioè la spesa (perché in macroeconomia la domanda non è un desiderio ma un acquisto) è la somma dei consumi delle famiglie, di quelli dello stato, delle spese per investimento degli imprenditori, delle spese che i non residenti fanno nel nostro paese (le nostre esportazioni), alle quali sottraiamo le importazioni, perché sono spese che noi facciamo in altri paesi, e quindi generano reddito in quei paesi, e non nel nostro.
Da qui deriva l'ovvia relazione:
Y = C + G + I + X - M
che si legge: il Pil è uguale alla somma della spesa per consumi (privati e pubblici), investimenti e esportazioni, meno le importazioni.
Bene: ora voi vi ricordate che se porto una cosa dall'altra parte dell'uguale il segno cambia, no? Non mi fate come Uga, vero (che ancora non deve effettuare questo doloroso passaggio, ma io già me lo pregusto: Vorfreude ist die schoenste Freude...).
Ecco, allora portiamo un po' di cosette a sinistra (operazione di questi tempi piuttosto difficile):
Y - C - G - I = X - M
Ora, ricordiamoci di una cosa molto semplice: cos'è il risparmio? Quello che si guadagna, meno quello che si consuma. Succede a noi singolarmente, e ci succede anche collettivamente. In altri termini, in contabilità nazionale il risparmio nazionale è S = Y - C - G. Se sostituiamo questa definizione, abbiamo la formuletta magica che fa capire tante cose:
S - I = X - M
ovvero: lo scarto fra risparmio nazionale e investimento nazionale (il risparmio "netto" di un paese) corrisponde allo scarto fra esportazioni e importazioni (le esportazioni "nette" di un paese, cioè il suo saldo commerciale).
Ne consegue che se in un paese X-M ha un valore abnorme, come accade in Germania con grande gioia di tutti, americani compresi, necessariamente dall'altra parte o il risparmio è altissimo (ma questo significa che il consumi devono essere rasoterra), o, se i consumi sono fisiologici (e quindi è tale anche il risparmio) dovranno essere bassini gli investimenti. Non si scappa: non è nemmeno matematica (che potrebbe essere un'opinione, come i miei amici matematici esperti di congetture sanno): è aritmetica, esiccome i numeri naturali pare li abbia creati Dio, credo che da essi sia più difficile sfuggire che dalla morte.
Infatti:
Qui avete la media sul periodo 1999-2007 (dall'entrata nell'euro allo scoppio della crisi) del rapporto fra investimenti fissi lordi e Pil). Le fonti sono il WEO per gli investimenti totali e AMECO per quelli in fabbricati residenziali (dwellings). Ora, se ci fate caso, la Germania si piazza ultima come rapporto investimenti/Pil sia in termini totali (l'intera barra) sia escludendo gli investimenti residenziali (cioè considerando la sola barra blu). Pensate che in termini di investimenti non residenziali riesce ad essere, se pure di un pelo, sotto alla Grecia. I due paesi con il maggior livello di investimenti non residenziali sono Austria e Portogallo (guarda te)! E, comunque, anche in questa classifica, come in quella della spesapubblicaimproduttiva, stanno peggio dell'Italia solo paesi virtuosi: la Finlandia, l'Olanda, la Francia e la Germania...
Ma non è che c'è qualcosa della virtù che ci sfugge? A noi non so, ai piddini di sicuro.
E la morale della favola qual è? Che da che mondo è mondo, nella maggior parte dei casi non si diventa competitivi "investendo", ma in un modo molto più semplice e che alle élite tedesche viene tanto naturale (come ricorda l'imprescindibile libro di Vladimiro): fottendo il prossimo.
Amen.
sabato 30 novembre 2013
Produttività, salari, crisi, logaritmi, marziani, onestà.
A Pescara vi avevo fatto vedere due grafici, uno tratto da Rick Wolff (2010), "In capitalist crisis rediscovering Marx", Socialism and democracy, 24, 130-146 (se non avete accesso a una biblioteca universitaria online, il testo potete trovarlo sul sito di Wolff ma senza il grafico), e uno tratto da Carmen Reinhart e Belen Sbrancia (2011) "The liquidation of government debt", BIS Working Papers, 363. L'accostamento di questi due grafici mi sembrava abbastanza istruttivo, per capire la fase storica che stiamo vivendo. Ve li ripropongo nell'ordine:
Quale messaggio convogliavano queste due immagini?
Quello che le due principali crisi debitorie dell'ultimo secolo (quella del 1929 e quella del 2008) sono state precedute da periodi più o meno lunghi nei quali i salari in termini reali (il potere d'acquisto dei lavoratori) erano stagnanti, mentre la produttività media del lavoro (la quantità di prodotto per addetto) aumentava. Ora, pare che perfino Cuperlo abbia capito che il capitalismo funziona finché c'è domanda (la famosa metafora dei 100 caffè sul bancone del barista, che dobbiamo al buon Alessandro Guerani). Ma la "domanda" in macroeconomia non è un mero desiderio. La domanda aggregata della quale si parla in macroeconomia è domanda effettiva, domanda che si traduce in capacità di spesa. Se il potere d'acquisto dei lavoratori si sviluppa di pari passo alla loro produttività, la domanda potrà essere finanziata dai redditi dei lavoratori stessi. Ma se la produttività cresce più in fretta dei salari reali, allora ci saranno in giro più prodotti che redditi da lavoro per acquistarli. Il capitalismo questo ovviamente lo sa, e pone rapidamente rimedio. Come? Semplice! Col debito.
Quando la dinamica dei salari reali è compressa, il cuneo fra produzione da acquistare e redditi percepiti da spendere deve essere colmato dal debito: fino a qui la contabilità, alla quale non si sfugge.
L'ideologia comincia quando devi scegliere se usare debito pubblico o debito privato. Ma il problema comunque è a monte: nella decisione di adottare una distribuzione del redditonon conforme alle logiche teoriche dell'economia di mercato da libro di testo. Perché nei libri di testo è scritto che il produttore massimizza il profitto mantenendo la remunerazione reale del lavoro proporzionale alla produttività del lavoro stesso. Per i clerici, con rendimenti di scala costanti il teorema di Eulero garantisce in questo caso che il prodotto venga distribuito senza residui. Per i beati, basta che abbiate capito fino alla penultima frase. Se volete approfondire nel dettaglio quello che è successo negli States, c'è questo.
Visto che ultimamente vi ho tenuto un po' a stecchetto di tecnica, aggiungo a seguire due perle tecniche, che vi aiuteranno a capire meglio un certo tipo di economisti.
Emiliano replicò con una garbata risposta nella quale mi dava sostanzialmente dell'incompetente (sempre con molto garbo, cosa che io apprezzo), sentenziando "Qualcuno forse ritiene che in fondo conti solo il salario reale, e che la quota salari non sia importante? Spero che nessuno si azzardi a pensarla in questi termini: la dinamica delle quote distributive è forse l’indicatore chiave del cambiamento nella struttura socio-politica di un paese."
Notate il simpatico atteggiamento da guardiano dell'ortodossia: "spero che nessuno ecc."! Ora, la domanda sorge spontanea: ma Rick Wolff, che scrive su Socialism and democracy, è anche lui, come me, un incompetente liberista "de passaggio"? Non lo so, ma a me pare di no. Dice di essere marxista, e ragiona anche da marxista (come poi vi mostrerò). Eppure il suo grafico riporta le stesse variabili del mio, e non quello che il nostro garbato guardiano dell'ortodossia ritiene sia l'indicatore chiave (nientemeno!).
Come si spiega questo mistero? Come si giustifca questa inspiegabile trascuratezza?
Semplice.
Col manuale di Acocella.
Vi spiego l'arcano usando appunto la terminologia di quel manuale: un manuale che uso nei corsi di laurea in economia aziendale, al terzo anno, per spiegare quello che evidentemente non tutti i partecipanti al dibattito hanno ancora interiorizzato.
Allora: se chiamiamo w la massa salariale in termini nominali e p l'indice dei prezzi, la massa salariale in termini reali è w/p (salario nominale diviso indice dei prezzi). w/p,insomma, indica il potere d'acquisto distribuito sotto forma di salari. Se chiamiamo N gli occupati, allora (w/p)/N è il salario reale per addetto, cioè, guarda un po', la riga rossa nel grafico di Wolff (Wolff divide per il numero di ore lavorate, che è una cosa più corretta e raffinata, ma la sostanza non cambia: basta pensare che l'occupazione N invece che in "teste" venga misurata appunto in ore lavorate e l'algebra resta la stessa).
E la produttività? La produttività media del lavoro è y/N, cioè il prodotto (in termini reali, cioè depurato dall'effetto dell'inflazione) diviso per gli occupati.
Ora, guardate cosa succede se dividiamo il salario reale per addetto per la produttività media del lavoro:
O poffarbacco poffarbacchissimo! Cosa abbiamo a destra dell'uguale? Ma il rapporto fra la massa salariale, w, e il prodotto in termini nominali, py. Quest'ultimo si ottiene moltiplicando la quantità di beni prodotti (y) per il loro prezzo medio (p). Ora, caso vuole che in una economia di mercato, nella quale si produce per vendere, il prodotto nominale coincida, guarda un po', col totale dei redditi nominali, e quindi a destra dell'uguale cosa abbiamo?
È lei o non è lei?
Ma cerrrrrrto che è lei: la quota salari!
Perché la quota salari è appunto il rapporto fra il monte salari (nominali) e il totale dei redditi (nominali), o, ciò che algebricamente è lo stesso, il rapporto fra salari (reali) unitari e produttività media del lavoro. Eh già! Quindi il rapporto fra la riga rossa e quella blu nel grafico di Wolff (o fra quella blu e quella rossa nel grafico mio) fornisce appunto la quota salari.
Ve lo dico in un altro modo.
Il mio grafico forniva il numeratore e il denominatore del rapporto che chiamiamo quota salari. Quindi il mio grafico, o se volete quello di Wolff, forniva più informazioni di quelle richieste dal mio gentile collega, non meno. Secondo voi, lui, di questo, se n'è accorto o no? E nel caso non se ne sia accorto, io cosa dovrei pensare di lui? E nel caso se ne fosse accorto, voi cosa dovreste pensare di lui?
In ogni caso, il punto sollevato era inconsistente, perché come poi ho mostrato qui certo, la svalutazione del 1992 non era stata una passeggiata di salute per i lavoratori italiani, ma era pressoché impercettibile se confrontata al crollo della quota salari che si era verificato dal 1976 in poi.
Aggiungo una osservazione.
Quando un rapporto (la quota salari) diminuisce, può essere che sia perché il numeratore (il salario reale per addetto) cala, o perché il denominatore (la produttività media del lavoro) cresce, o per una qualsiasi combinazione di questi fattori. Non è del tutto irrilevante capire cosa sta succedendo. Ad esempio, ormai sapete che dalla fine degli anni '70 a metà degli anni '90 il rapporto è diminuito perché i salari reali sono rimasti stazionari, mentre la produttività aumentava. Dalla metà degli anni '90 il rapporto è rimasto stazionario perché ha smesso di crescere anche il denominatore (la produttività, come abbiamo illustrato qui).
Non è strano che qualcuno ti confuti affermando che il tuo grafico non dà le informazioni giuste, quando in realtà le dà, e anzi ne dà di più? Sì, è strano, mi sembrava molto strano, all'inizio, ma mi ci son dovuto abituare, anche perché, andando avanti, comincio a comprenderne le ragioni.
Tutto comprendere è tutto perdonare. E forse anche voi avrete compreso, da questo semplice esempio, perché certe volte non mi soffermo a confutare certi argomenti. Fidatevi: se non lo faccio è perché non sempre ne vale esattamente la pena...
Eh, ragazzi, qui son dolori! Ma visto che volete diventare tecnici, vi toccherà fare un salto indietro nel tempo, tornando sui banchi di scuola, o meglio, grazie all'INVALSI, di sQuola...
Allora, prendiamola un po' larga.
Il logaritmo in base x del numero y è l'esponente z al quale bisogna elevare la base per ottenere il numero dato.
Dio, che mal di testa. Sì, lo so. Però se volete capire quanto può essere furbetto un marziano, dovete affrontare questo doloroso passo.
Prendiamo tre numeri: 10, 100 e 1000, per esempio, e consideriamo la base 10.
Ora, succede questo:
Cioè: siccome 10 alla prima è uguale a 10, il logaritmo in base dieci di dieci è uno. Siccome dieci alla seconda è uguale a 100, il logaritmo in base dieci di 100 è 2. Siccome dieci alla terza è uguale a mille, il logaritmo in base 10 di 1000 è 3.
Notate bene: da una parte abbiamo dei numeri che crescono rapidamente, esponenzialmente: 10, 100, 1000. Ma i logaritmi di questi numeri sono numeri che crescono molto più lentamente, linearmente: 1, 2, 3. Notate anche un'altra cosa. I numeri 10, 100, 1000 crescono a un tasso di crescita percentuale costante del 900%. Esempio: (100-10)/10=9=900%, (1000-100)/100=9=900%. I numeri 1, 2, 3 crescono con unincremento (non percentuale) costante: 2-1 = 1, 3-2 = 1.
Poi vi spiego a cosa serve.
Prima, cerco di farvi intuire un'altra cosa. Supponiamo che una variabile y cresca a un tasso costante n. Succederà una cosa del genere:
Cioè: se al tempo zero la variabile vale un certo valore y soprassegnato, al tempo uno questo valore sarà moltiplicato per uno più il tasso di crescita, al tempo due per uno più il tasso di crescita elevato al quadrato, ecc. Insomma: la formula dell'interesse composto, avete presente? Volete un esempio? Ecco, ve lo fornisco qui:
Se il tasso è del 5% (cioè 0.05) e il valore iniziale è 1, al tempo1 y=1x1.05, al tempo 2y=1.05x1.05=1.103, ecc. Ora, notate una cosa. Se una variabile cresce a un tasso percentuale di crescita costante, la sua crescita sarà esponenziale. Guarda caso, questo è quello che succede di norma alle variabili in economia (almeno nei modelli teorici, ma spesso anche in pratica). Guardate cosa fa la variabile del nostro esempio se andiamo avanti fino al tempo t=100:
Ma guarda un po'! Sembra proprio, a grandi linee, l'andamento della produttività media nel grafico di Wolff. È strano? No, perché, come vi ho detto, di norma in economia le variabili crescono a tassi percentuali più o meno costanti.
E ora applichiamo la magia dei logaritmi. Se noi, di questa serie che è esponenziale, prendiamo il logaritmo, cosa succederà? Lo abbiamo visto sopra. Il logaritmo trasforma dei numeri che crescono a tasso percentuale costante, e quindi hanno un andamento esponenziale, in altri numeri che crescono a incremento costante, e quindi hanno un andamento lineare. E quindi? E quindi il logaritmo (in base 10) della serie rappresentata qua sopra sarà questo:
Vedete? I conti tornano. Quando la serie originale vale 1, il logaritmo vale 0 (perché qualsiasi numero elevato alla zero dà uno: se non vi ricordate perché, ve lo spiegherà - male - uno dei tanti ingengnieri... e vi va ancora bene, perché se invece ve lo spiegasse un matematico...). Poi, quando la serie originale arriva a 10 (al tempo 48) il suo logaritmo vale 1 (e sopra vi ho spiegato perché), e quando arriva a 100 (intorno al tempo 95) il suo logaritmo vale 2.
I conti tornano, il che, ovviamente, non vi esenta, in linea di principio, dal chiosare questo mio sforzo didattico con un sentito: "Mastica!"
(per i non romani: "Mastica!" sta per "ma sti cazzi?", ovvero: "e che me ne cale?", mentre "Giamaica!" sta per "già m'hai cacato er cazzo!", ovvero: "cominci ad indispormi!")
Ma io, incurante del vostro sbigottimento, rincaro la dose, e vi faccio vedere un'altra cosa. Il logaritmo della nostra y preso in base e. Ora, cosa sia il numero e ve lo leggete qui. Io cerco di spiegarvi a cosa serve agli economisti. Guardate:
E a questo punto costernati penserete: "Ecco qua, se lo semo ggiocato! Ha lavorato troppo, so' ddue anni che sse fa er culo, e alla fine doveva succede: ha sbroccato. Ce fa vvede' ddu grafici uguali come si fussero diversi...".
Aspettate: io sono sbroccato, ma perché modestamente lo nacqui. Io due grafici però uguali non sono. Guardate l'asse delle ordinate (quello verticale, come caritatevolmente soggiungo ai miei studenti della specialistica onde far sparire dai loro volti quello sbigottimento che me li rende tanto cari...).
Nel grafico precedente (log in base 10) andava da 0 a 2 (i conti tornano, visto che la serie andava da 0 a un po' più di 100). Nel grafico del log in base e invece va da 0 a 5, e anche qui i conti tornano: siccome la base è più piccola (2 è più piccolo di 10) l'esponente cui è necessario elevarla per arrivare a 100 è più grande.
E fino a qui, ancora mastica.
Ok. Però... abbiamo 100 osservazioni, che vanno da 0 a 5 in modo lineare. L'incremento totale, sulle 100 osservazioni (dopo un secolo, se le osservazioni sono anni), è pari a 5. Se lo dividiamo per il numero delle osservazioni (cioè, sempre per fissare le idee, degli anni) riscontriamo che l'incremento fra t e t+1, cioè da un anno all'altro, del logaritmo in base e della nostra serie è 5/100=0.05.
Oooops!
Quindi il logaritmo in base e trasforma una serie che cresce esponenzialmente a un tasso percentuale del 5% in una serie che cresce linearmente con un incremento costante di 0.05. Insomma: se abbiamo un grafico logaritmico in base e, l'incremento della serie (la pendenza del grafico) corrisponde al suo tasso percentuale di crescita. Una cosa che in economia torna utile.
Ora vi faccio vedere un'altra cosa. Supponiamo che invece y cresca al 20%. Avete presente l'inflazzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzione a due cifre? Ecco, una cosa del genere. Potete pensare a y come a un indice dei prezzi che cresce con un tasso di inflazione del 20% all'anno. Cosa succederà, in questo caso? Guardiamo il grafico della serie:
Oibo'! Ma la serie non cresce più! Cresce solo alla fine!
Un attimo. Siccome una serie che cresce del 20% all'anno (partendo da uno) dopo un secolo supera gli 80 milioni, è chiaro che le osservazioni iniziali saranno tutte schiacciate sull'asse delle ascisse. Sembrano appiattite, perché il valore finale è molto alto, ma questo non vuol dire che all'inizio la variabile non cresca. Vuol dire solo che devi prendere i logaritmi. Se lo fai, vedi questo:
E così si capisce che la serie cresce a un tasso percentuale costante, di circa il 20% (vedete che dopo 100 osservazioni arriva a 0.2x100=20: il dato è approssimato, sarebbe lungo spiegarvi perché, ma accontentatevi, o studiate analisi 1).
Sapete quante volte, alla Sapienza, il "povero studente" veniva da me con un grafico come il penultimo, e mi diceva: "Professore, i dati non ci sono". E io: "Benedetto figliuolo (tradotto: povero coglione), ma se mi stai plottando l'indice dei prezzi al consumo dell'Argentina, con inflazione a quattro cifre, mi pare abbastanza chiaro che non vedrai nulla se non prendi i logaritmi, no?". Lui non capiva, prendeva i logaritmi, e pensava che io avessi poteri taumaturgici.
Se vi volete divertire a fare i conti, il foglio Excel è qui. Mettete nella casella gialla vari tassi di crescita (ricordando che non sono inseriti come percentuali, per cui 0.05=5%, quindi 5=500%), e divertitevi a vedere cosa succede.
Allora, ora che abbiamo la tecnica, possiamo passare all'ideologia. Perché anche del logaritmo si può fare un uso, o un non uso, ideologico.
Pensateci bene. Cosa vuole dimostrarci un marZiano (o meglio, un marZista, ma marZiano torna meglio)? Vuole dimostrarci che ha ragione lui, e fino a qui lo sentiamo nostro fratello: abbiamo un obiettivo comune. E in che modo vuole avere ragione? Semplice! Nel dimostrarci che il capitalismo sta alla frutta, che ormai le sue insanabili contraddizioni lo hanno portato sull'orlo del baratro finale, che la palingenesi si sta avvicinando.
Bene.
Qui scatta il non uso ideologico del logaritmo. Perché ovviamente se te ttu vvòi dimostrare che un fenomeno (ad esempio, il capitalismo) è inserito in una dinamica esplosiva, eviterai di utilizzare una trasformata (quella logaritmica) che linearizza gli esponenziali. Solo che in questo modo "schiaccerai" il fenomeno nella prima parte del grafico, quella più a sinistra, quella più antica. Il che ti torna anche comodo, perché così potrai verniciare la tua patacca con uno smalto che torna sempre comodo: lo smalto del "il mondo non è più quello di una volta, non ci sono più le mezze stagioni, e soprattutto c'è la Ciiiiiiiiiiiiiiiiiiina"...
Per farvi capire, mi sono ricostruito il grafico in casa. Non è stato semplicissimo e non ho trovato, nel poco tempo a disposizione, esattamente gli stessi dati di Wolff, ma le dinamiche son quelle, come vedrete, e vedrete anche che con i dati di Wolff il mio punto sarebbe ancora più evidente.
Dunque: questo è il mio grafico:
La serie della produttività coincide con quella di Wolff fino al 1969 ed è tratta da qui, poi dal 1969 al 1987 ho usato la serie del non farm business, perché non ho trovato ilmanufacturing, e poi dal 1987 a oggi ho usato il manufacturing, e i dati vengono da qui. Per i salari reali ho usato i dati del Two Charlie's paper, che non è l'articolo dei due vietnamiti, ma l'articolo di Nelson e Plosser, uno degli articoli più famosi nella storia della macroeconomia recente. I dati li trovate qui.
Ora, anche se le fonti sono diverse, il messaggio è lo stesso. Prima di dirvelo, vi faccio notare le differenze. Intanto, il mio indice di produttività arriva a 1600 anziché oltre 1800 come quello di Wolff, per due motivi. Il primo è che i miei dati partono dal 1900, anziché dal 1890 (i dati di Nelson e Plosser partono dal 1900 e non avevo voglia di ricostruire e caricare a mano dieci anni di salari reali: sì, sono un lavoratore pubblico improduttivo); secondo, dal 1969 al 1987 non ho trovato la produttività del manufacturing, e quindi in quel periodo la serie cresce leggermente di meno. Circa i salari, il comportamento è pressoché identico.
L'unica differenza sensibile è che coi dati di Wolff nel 1947 i due indici tornano a coincidere, mentre nei miei dati rimangono scostati, ma la caratteristica più rilevante, cioè lo stacco della produttività a partire dagli anni '70, rimane il medesimo.
Che succede, però, se rappresentiamo le serie prendendone i logaritmi naturali?
Succede questo:
Viste così, le dinamiche che stiamo vivendo, pur restando esplosive, sembrano un po' meno inusuali.
Intanto, una stagnazione del salari si era già avuta a partire dal 1920, ed era durata sostanzialmente fino allo scoppio della Seconda guerra mondiale. In questo periodo, l'indice della produttività ha staccato quello dei salari fino a un massimo di circa il 60%, corrispondente a un po' più di una "tacca" sull'asse delle ordinate (nel 1935). Dopo la guerra i due indici sono cresciuti in parallelo (ma i salari sono rimasti un po' sotto, questo si vede sia nel grafico di Wolff che nel mio). La produttività ha preso di nuovo il "fugone" all'inizio degli anni '80, e da allora l'ulteriore stacco rispetto all'indice dei salari reali è stato di circa il 90% (corrispondente a un po' meno di due tacche sull'asse delle ordinate).
Certo, le dimensioni del fenomeno sono molto maggiori, questo è palese. D'altra parte, oggi il capitalismo non può sfogare le sue tensioni, come ai bei (per lui) tempi andati, scatenando qualche simpatica guerra mondiale, e poi la finanziarizzazione dell'economia è progredita, e anche il keynesismo ci ha messo del suo. La politica fiscale espansiva (di Reagan o di Craxi, con segno, colore e intenzioni diverse) ha messo una bella toppa al cuneo fra salari e produttività negli anni '80, portando a una discreta crescita del debito pubblico negli Stati Uniti e in Italia. Una cosa simili, in fondo, era successa anche negli anni '20, come fa vedere il grafico di Belen e Sbrancia (vedi sopra). Poi, dagli anni '90, il testimone è passato all'indebitamento privato, sia negli Stati Uniti che da noi, e siamo andati avanti per un altro quindicennio. Questo anche concorre a spiegare perché gli squilibri distributivi, e quindi finanziari, accumulati, siano questa volta maggiori.
Ma da qui a dire che "this time it is different", mi dispiace, ma ce ne corre. Non è così "different" (in questo, purtroppo, hanno ragione loro), e quindi è piuttosto futile aspettarsi palingenesi, e piuttosto furbesco suggerire imminenti collassi del sistema, semplicemente usando unità di misura opinabili!
Ora, io, logaritmi a parte, con l'analisi di Wolff, come con quella di certi marZiani "de noantri" (che prima ti dileggiano e poi ce vanno in puzza), mi ritrovo, assolutamente.
La terapia mi lascia un po' perplesso, perché la vedo sottoposta a due ovvie obiezioni:
1) e se ci dicono di no?
2) e i soldi chi ce li mette?
Cioè, come funziona? Ci svegliamo un giorno, andiamo al lavoro, e diciamo agli amministratori: "Scusate, andatevene a casa, che ora decidiamo noi". Loro se ne vanno, e gli azionisti come la prendono? E le banche cosa fanno? Ah, certo, ma nel frattempo avremo fatto lo stesso anche nelle banche. In simultanea. Be', certo... Son quelle cose un po' così, come avere la luna in trigono con Venere, Mercurio in quadratura con Saturno e Giove in opposizione con Marte: opportunità che si presentano (se possibile) una volta nella vita, e che sarebbe in effetti stupido non sfruttare.
Ragazzi, non so come dirvelo: io vorrei tanto credere che sia possibile avere un mondo migliore... Ma se le proposte sono queste, alla fine preferisco rendere meno peggiore quello nel quale sono nato. Mi scuserete, oppure, deponendo linguaggio liturgico e puzza sotto il naso, mi direte dove sbaglio, e io cercherò di capirlo...
Ad esempio, ascoltatevi questo. Ich will den Kreuzstab gerne tragen: porterò con gioia la croce (che viene dalle mani del Signore). Anche se avete le orecchie devastate dalla musica cessica che ascoltate tutto il santo giorno, lo sentite che su Kreuz c'è una nota molto espressiva? Bach usa un intervallo strano, una seconda eccedente (si bemolle-do diesis, non sto parlando di tette ma di note). E anche qui, uno direbbe: "Bello, sì, forse, ma comunque mastica...".
E invece no, perché c'è il dettaglio (che fa la gioia dell'intenditore). Guardate com'è scritto:
Visto? Per aumentare la seconda, rendendola eccedente, Bach mette un diesis, che sarebbe questo segno # (er cancelletto), sul do che corrisponde alla parola Kreuz. Ora, siccome a quei tempi Twitter non c'era, difficilmente Bach avrà voluto creare l'hashtag #kreuz. Il fatto è un altro: il diesis in effetti è una croce. Insomma: Bach usa il segno grafico dell'alterazione per simboleggiare il concetto espresso dal testo, e sicuramente non lo fa per caso. Vi risparmio altri simboli, come il peso della croce, simbolizzato da un vocalizzo di otto battute sulla a di tragen, ecc. Dal che si evince che qualche volta le seghe mentali possono portare a risultati esteticamente appaganti. Un giorno in cui anche a voi, come a me, la croce che vi siete scelti comincerà a pesare un po' sulle spalle, ricordatevi di questo link, e poi ripartite di slancio.
Noi la croce la portiamo, gerne, ma non è detto che sia destinata a noi stessi.
La prima è che
La Nature est un temple où des vivants piliers
laissent parfois sortir des confuses paroles ;
l'homme y passe à travers des forêts de symboles
qui l'observent avec des regards familier.
e quindi, in queste circostanze,
Con gli ambiziosi madre Natura sarà sempre matrigna, e ai superbi e agli incolti nasconderà i suoi rutilanti colori. Insomma: poveri piddini, non sanno cosa si perdono. E per chi non avesse, da madre Natura, ricevuto il dono incomparabile di leggere fra le righe, suggerisco sommessamente questa chiave di lettura.
Quale messaggio convogliavano queste due immagini?
Quello che le due principali crisi debitorie dell'ultimo secolo (quella del 1929 e quella del 2008) sono state precedute da periodi più o meno lunghi nei quali i salari in termini reali (il potere d'acquisto dei lavoratori) erano stagnanti, mentre la produttività media del lavoro (la quantità di prodotto per addetto) aumentava. Ora, pare che perfino Cuperlo abbia capito che il capitalismo funziona finché c'è domanda (la famosa metafora dei 100 caffè sul bancone del barista, che dobbiamo al buon Alessandro Guerani). Ma la "domanda" in macroeconomia non è un mero desiderio. La domanda aggregata della quale si parla in macroeconomia è domanda effettiva, domanda che si traduce in capacità di spesa. Se il potere d'acquisto dei lavoratori si sviluppa di pari passo alla loro produttività, la domanda potrà essere finanziata dai redditi dei lavoratori stessi. Ma se la produttività cresce più in fretta dei salari reali, allora ci saranno in giro più prodotti che redditi da lavoro per acquistarli. Il capitalismo questo ovviamente lo sa, e pone rapidamente rimedio. Come? Semplice! Col debito.
Quando la dinamica dei salari reali è compressa, il cuneo fra produzione da acquistare e redditi percepiti da spendere deve essere colmato dal debito: fino a qui la contabilità, alla quale non si sfugge.
L'ideologia comincia quando devi scegliere se usare debito pubblico o debito privato. Ma il problema comunque è a monte: nella decisione di adottare una distribuzione del redditonon conforme alle logiche teoriche dell'economia di mercato da libro di testo. Perché nei libri di testo è scritto che il produttore massimizza il profitto mantenendo la remunerazione reale del lavoro proporzionale alla produttività del lavoro stesso. Per i clerici, con rendimenti di scala costanti il teorema di Eulero garantisce in questo caso che il prodotto venga distribuito senza residui. Per i beati, basta che abbiate capito fino alla penultima frase. Se volete approfondire nel dettaglio quello che è successo negli States, c'è questo.
Visto che ultimamente vi ho tenuto un po' a stecchetto di tecnica, aggiungo a seguire due perle tecniche, che vi aiuteranno a capire meglio un certo tipo di economisti.
Produttività, salario reale, quota salari.
Il grafico di Wolff, se ci fate caso, riporta gli stessi dati della figura 37 del mio libro, corrispondende alla figura 7 di questo post. Forse ricorderete che nella mia lettera a Brancaccio citai lo stesso grafico per argomentare che la sua conclusione che la flessibilità del cambio sarebbe necessariamente tornata a svantaggio dei lavoratori era quanto meno avventata, non solo alla luce dei modelli teorici, ma anche dell'esperienza storica, in particolare di quella che tutti dovremmo ricordare perché a noi più vicina: quella dell'Italia. Negli anni in cui la lira perdeva terreno (gli anni '70) chissà perché il potere d'acquisto dei lavoratori cresceva...Emiliano replicò con una garbata risposta nella quale mi dava sostanzialmente dell'incompetente (sempre con molto garbo, cosa che io apprezzo), sentenziando "Qualcuno forse ritiene che in fondo conti solo il salario reale, e che la quota salari non sia importante? Spero che nessuno si azzardi a pensarla in questi termini: la dinamica delle quote distributive è forse l’indicatore chiave del cambiamento nella struttura socio-politica di un paese."
Notate il simpatico atteggiamento da guardiano dell'ortodossia: "spero che nessuno ecc."! Ora, la domanda sorge spontanea: ma Rick Wolff, che scrive su Socialism and democracy, è anche lui, come me, un incompetente liberista "de passaggio"? Non lo so, ma a me pare di no. Dice di essere marxista, e ragiona anche da marxista (come poi vi mostrerò). Eppure il suo grafico riporta le stesse variabili del mio, e non quello che il nostro garbato guardiano dell'ortodossia ritiene sia l'indicatore chiave (nientemeno!).
Come si spiega questo mistero? Come si giustifca questa inspiegabile trascuratezza?
Semplice.
Col manuale di Acocella.
Vi spiego l'arcano usando appunto la terminologia di quel manuale: un manuale che uso nei corsi di laurea in economia aziendale, al terzo anno, per spiegare quello che evidentemente non tutti i partecipanti al dibattito hanno ancora interiorizzato.
Allora: se chiamiamo w la massa salariale in termini nominali e p l'indice dei prezzi, la massa salariale in termini reali è w/p (salario nominale diviso indice dei prezzi). w/p,insomma, indica il potere d'acquisto distribuito sotto forma di salari. Se chiamiamo N gli occupati, allora (w/p)/N è il salario reale per addetto, cioè, guarda un po', la riga rossa nel grafico di Wolff (Wolff divide per il numero di ore lavorate, che è una cosa più corretta e raffinata, ma la sostanza non cambia: basta pensare che l'occupazione N invece che in "teste" venga misurata appunto in ore lavorate e l'algebra resta la stessa).
E la produttività? La produttività media del lavoro è y/N, cioè il prodotto (in termini reali, cioè depurato dall'effetto dell'inflazione) diviso per gli occupati.
Ora, guardate cosa succede se dividiamo il salario reale per addetto per la produttività media del lavoro:
O poffarbacco poffarbacchissimo! Cosa abbiamo a destra dell'uguale? Ma il rapporto fra la massa salariale, w, e il prodotto in termini nominali, py. Quest'ultimo si ottiene moltiplicando la quantità di beni prodotti (y) per il loro prezzo medio (p). Ora, caso vuole che in una economia di mercato, nella quale si produce per vendere, il prodotto nominale coincida, guarda un po', col totale dei redditi nominali, e quindi a destra dell'uguale cosa abbiamo?
È lei o non è lei?
Ma cerrrrrrto che è lei: la quota salari!
Perché la quota salari è appunto il rapporto fra il monte salari (nominali) e il totale dei redditi (nominali), o, ciò che algebricamente è lo stesso, il rapporto fra salari (reali) unitari e produttività media del lavoro. Eh già! Quindi il rapporto fra la riga rossa e quella blu nel grafico di Wolff (o fra quella blu e quella rossa nel grafico mio) fornisce appunto la quota salari.
Ve lo dico in un altro modo.
Il mio grafico forniva il numeratore e il denominatore del rapporto che chiamiamo quota salari. Quindi il mio grafico, o se volete quello di Wolff, forniva più informazioni di quelle richieste dal mio gentile collega, non meno. Secondo voi, lui, di questo, se n'è accorto o no? E nel caso non se ne sia accorto, io cosa dovrei pensare di lui? E nel caso se ne fosse accorto, voi cosa dovreste pensare di lui?
In ogni caso, il punto sollevato era inconsistente, perché come poi ho mostrato qui certo, la svalutazione del 1992 non era stata una passeggiata di salute per i lavoratori italiani, ma era pressoché impercettibile se confrontata al crollo della quota salari che si era verificato dal 1976 in poi.
Aggiungo una osservazione.
Quando un rapporto (la quota salari) diminuisce, può essere che sia perché il numeratore (il salario reale per addetto) cala, o perché il denominatore (la produttività media del lavoro) cresce, o per una qualsiasi combinazione di questi fattori. Non è del tutto irrilevante capire cosa sta succedendo. Ad esempio, ormai sapete che dalla fine degli anni '70 a metà degli anni '90 il rapporto è diminuito perché i salari reali sono rimasti stazionari, mentre la produttività aumentava. Dalla metà degli anni '90 il rapporto è rimasto stazionario perché ha smesso di crescere anche il denominatore (la produttività, come abbiamo illustrato qui).
Non è strano che qualcuno ti confuti affermando che il tuo grafico non dà le informazioni giuste, quando in realtà le dà, e anzi ne dà di più? Sì, è strano, mi sembrava molto strano, all'inizio, ma mi ci son dovuto abituare, anche perché, andando avanti, comincio a comprenderne le ragioni.
Tutto comprendere è tutto perdonare. E forse anche voi avrete compreso, da questo semplice esempio, perché certe volte non mi soffermo a confutare certi argomenti. Fidatevi: se non lo faccio è perché non sempre ne vale esattamente la pena...
Marx, i logaritmi, e la crisi del capitalismo.
Alla conferenza di Pescara vi ho fatto notare un dettaglio del grafico di Wolff: non usa la scala logaritmica. Cosa c'entra, direte voi, e soprattutto cosa sono i logaritmi, a cosa servono?Eh, ragazzi, qui son dolori! Ma visto che volete diventare tecnici, vi toccherà fare un salto indietro nel tempo, tornando sui banchi di scuola, o meglio, grazie all'INVALSI, di sQuola...
Allora, prendiamola un po' larga.
Il logaritmo in base x del numero y è l'esponente z al quale bisogna elevare la base per ottenere il numero dato.
Dio, che mal di testa. Sì, lo so. Però se volete capire quanto può essere furbetto un marziano, dovete affrontare questo doloroso passo.
Prendiamo tre numeri: 10, 100 e 1000, per esempio, e consideriamo la base 10.
Ora, succede questo:
Cioè: siccome 10 alla prima è uguale a 10, il logaritmo in base dieci di dieci è uno. Siccome dieci alla seconda è uguale a 100, il logaritmo in base dieci di 100 è 2. Siccome dieci alla terza è uguale a mille, il logaritmo in base 10 di 1000 è 3.
Notate bene: da una parte abbiamo dei numeri che crescono rapidamente, esponenzialmente: 10, 100, 1000. Ma i logaritmi di questi numeri sono numeri che crescono molto più lentamente, linearmente: 1, 2, 3. Notate anche un'altra cosa. I numeri 10, 100, 1000 crescono a un tasso di crescita percentuale costante del 900%. Esempio: (100-10)/10=9=900%, (1000-100)/100=9=900%. I numeri 1, 2, 3 crescono con unincremento (non percentuale) costante: 2-1 = 1, 3-2 = 1.
Poi vi spiego a cosa serve.
Prima, cerco di farvi intuire un'altra cosa. Supponiamo che una variabile y cresca a un tasso costante n. Succederà una cosa del genere:
Cioè: se al tempo zero la variabile vale un certo valore y soprassegnato, al tempo uno questo valore sarà moltiplicato per uno più il tasso di crescita, al tempo due per uno più il tasso di crescita elevato al quadrato, ecc. Insomma: la formula dell'interesse composto, avete presente? Volete un esempio? Ecco, ve lo fornisco qui:
Se il tasso è del 5% (cioè 0.05) e il valore iniziale è 1, al tempo1 y=1x1.05, al tempo 2y=1.05x1.05=1.103, ecc. Ora, notate una cosa. Se una variabile cresce a un tasso percentuale di crescita costante, la sua crescita sarà esponenziale. Guarda caso, questo è quello che succede di norma alle variabili in economia (almeno nei modelli teorici, ma spesso anche in pratica). Guardate cosa fa la variabile del nostro esempio se andiamo avanti fino al tempo t=100:
Ma guarda un po'! Sembra proprio, a grandi linee, l'andamento della produttività media nel grafico di Wolff. È strano? No, perché, come vi ho detto, di norma in economia le variabili crescono a tassi percentuali più o meno costanti.
E ora applichiamo la magia dei logaritmi. Se noi, di questa serie che è esponenziale, prendiamo il logaritmo, cosa succederà? Lo abbiamo visto sopra. Il logaritmo trasforma dei numeri che crescono a tasso percentuale costante, e quindi hanno un andamento esponenziale, in altri numeri che crescono a incremento costante, e quindi hanno un andamento lineare. E quindi? E quindi il logaritmo (in base 10) della serie rappresentata qua sopra sarà questo:
Vedete? I conti tornano. Quando la serie originale vale 1, il logaritmo vale 0 (perché qualsiasi numero elevato alla zero dà uno: se non vi ricordate perché, ve lo spiegherà - male - uno dei tanti ingengnieri... e vi va ancora bene, perché se invece ve lo spiegasse un matematico...). Poi, quando la serie originale arriva a 10 (al tempo 48) il suo logaritmo vale 1 (e sopra vi ho spiegato perché), e quando arriva a 100 (intorno al tempo 95) il suo logaritmo vale 2.
I conti tornano, il che, ovviamente, non vi esenta, in linea di principio, dal chiosare questo mio sforzo didattico con un sentito: "Mastica!"
(per i non romani: "Mastica!" sta per "ma sti cazzi?", ovvero: "e che me ne cale?", mentre "Giamaica!" sta per "già m'hai cacato er cazzo!", ovvero: "cominci ad indispormi!")
Ma io, incurante del vostro sbigottimento, rincaro la dose, e vi faccio vedere un'altra cosa. Il logaritmo della nostra y preso in base e. Ora, cosa sia il numero e ve lo leggete qui. Io cerco di spiegarvi a cosa serve agli economisti. Guardate:
E a questo punto costernati penserete: "Ecco qua, se lo semo ggiocato! Ha lavorato troppo, so' ddue anni che sse fa er culo, e alla fine doveva succede: ha sbroccato. Ce fa vvede' ddu grafici uguali come si fussero diversi...".
Aspettate: io sono sbroccato, ma perché modestamente lo nacqui. Io due grafici però uguali non sono. Guardate l'asse delle ordinate (quello verticale, come caritatevolmente soggiungo ai miei studenti della specialistica onde far sparire dai loro volti quello sbigottimento che me li rende tanto cari...).
Nel grafico precedente (log in base 10) andava da 0 a 2 (i conti tornano, visto che la serie andava da 0 a un po' più di 100). Nel grafico del log in base e invece va da 0 a 5, e anche qui i conti tornano: siccome la base è più piccola (2 è più piccolo di 10) l'esponente cui è necessario elevarla per arrivare a 100 è più grande.
E fino a qui, ancora mastica.
Ok. Però... abbiamo 100 osservazioni, che vanno da 0 a 5 in modo lineare. L'incremento totale, sulle 100 osservazioni (dopo un secolo, se le osservazioni sono anni), è pari a 5. Se lo dividiamo per il numero delle osservazioni (cioè, sempre per fissare le idee, degli anni) riscontriamo che l'incremento fra t e t+1, cioè da un anno all'altro, del logaritmo in base e della nostra serie è 5/100=0.05.
Oooops!
Quindi il logaritmo in base e trasforma una serie che cresce esponenzialmente a un tasso percentuale del 5% in una serie che cresce linearmente con un incremento costante di 0.05. Insomma: se abbiamo un grafico logaritmico in base e, l'incremento della serie (la pendenza del grafico) corrisponde al suo tasso percentuale di crescita. Una cosa che in economia torna utile.
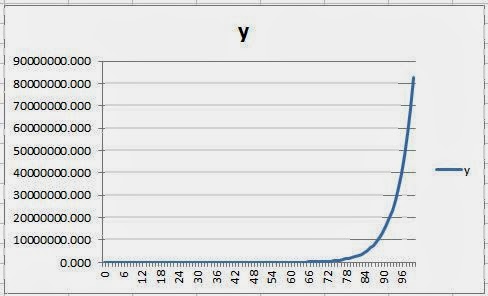
Ora vi faccio vedere un'altra cosa. Supponiamo che invece y cresca al 20%. Avete presente l'inflazzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzione a due cifre? Ecco, una cosa del genere. Potete pensare a y come a un indice dei prezzi che cresce con un tasso di inflazione del 20% all'anno. Cosa succederà, in questo caso? Guardiamo il grafico della serie:
Oibo'! Ma la serie non cresce più! Cresce solo alla fine!
Un attimo. Siccome una serie che cresce del 20% all'anno (partendo da uno) dopo un secolo supera gli 80 milioni, è chiaro che le osservazioni iniziali saranno tutte schiacciate sull'asse delle ascisse. Sembrano appiattite, perché il valore finale è molto alto, ma questo non vuol dire che all'inizio la variabile non cresca. Vuol dire solo che devi prendere i logaritmi. Se lo fai, vedi questo:
E così si capisce che la serie cresce a un tasso percentuale costante, di circa il 20% (vedete che dopo 100 osservazioni arriva a 0.2x100=20: il dato è approssimato, sarebbe lungo spiegarvi perché, ma accontentatevi, o studiate analisi 1).
Sapete quante volte, alla Sapienza, il "povero studente" veniva da me con un grafico come il penultimo, e mi diceva: "Professore, i dati non ci sono". E io: "Benedetto figliuolo (tradotto: povero coglione), ma se mi stai plottando l'indice dei prezzi al consumo dell'Argentina, con inflazione a quattro cifre, mi pare abbastanza chiaro che non vedrai nulla se non prendi i logaritmi, no?". Lui non capiva, prendeva i logaritmi, e pensava che io avessi poteri taumaturgici.
Se vi volete divertire a fare i conti, il foglio Excel è qui. Mettete nella casella gialla vari tassi di crescita (ricordando che non sono inseriti come percentuali, per cui 0.05=5%, quindi 5=500%), e divertitevi a vedere cosa succede.
Allora, ora che abbiamo la tecnica, possiamo passare all'ideologia. Perché anche del logaritmo si può fare un uso, o un non uso, ideologico.
Pensateci bene. Cosa vuole dimostrarci un marZiano (o meglio, un marZista, ma marZiano torna meglio)? Vuole dimostrarci che ha ragione lui, e fino a qui lo sentiamo nostro fratello: abbiamo un obiettivo comune. E in che modo vuole avere ragione? Semplice! Nel dimostrarci che il capitalismo sta alla frutta, che ormai le sue insanabili contraddizioni lo hanno portato sull'orlo del baratro finale, che la palingenesi si sta avvicinando.
Bene.
Qui scatta il non uso ideologico del logaritmo. Perché ovviamente se te ttu vvòi dimostrare che un fenomeno (ad esempio, il capitalismo) è inserito in una dinamica esplosiva, eviterai di utilizzare una trasformata (quella logaritmica) che linearizza gli esponenziali. Solo che in questo modo "schiaccerai" il fenomeno nella prima parte del grafico, quella più a sinistra, quella più antica. Il che ti torna anche comodo, perché così potrai verniciare la tua patacca con uno smalto che torna sempre comodo: lo smalto del "il mondo non è più quello di una volta, non ci sono più le mezze stagioni, e soprattutto c'è la Ciiiiiiiiiiiiiiiiiiina"...
Per farvi capire, mi sono ricostruito il grafico in casa. Non è stato semplicissimo e non ho trovato, nel poco tempo a disposizione, esattamente gli stessi dati di Wolff, ma le dinamiche son quelle, come vedrete, e vedrete anche che con i dati di Wolff il mio punto sarebbe ancora più evidente.
Dunque: questo è il mio grafico:
La serie della produttività coincide con quella di Wolff fino al 1969 ed è tratta da qui, poi dal 1969 al 1987 ho usato la serie del non farm business, perché non ho trovato ilmanufacturing, e poi dal 1987 a oggi ho usato il manufacturing, e i dati vengono da qui. Per i salari reali ho usato i dati del Two Charlie's paper, che non è l'articolo dei due vietnamiti, ma l'articolo di Nelson e Plosser, uno degli articoli più famosi nella storia della macroeconomia recente. I dati li trovate qui.
Ora, anche se le fonti sono diverse, il messaggio è lo stesso. Prima di dirvelo, vi faccio notare le differenze. Intanto, il mio indice di produttività arriva a 1600 anziché oltre 1800 come quello di Wolff, per due motivi. Il primo è che i miei dati partono dal 1900, anziché dal 1890 (i dati di Nelson e Plosser partono dal 1900 e non avevo voglia di ricostruire e caricare a mano dieci anni di salari reali: sì, sono un lavoratore pubblico improduttivo); secondo, dal 1969 al 1987 non ho trovato la produttività del manufacturing, e quindi in quel periodo la serie cresce leggermente di meno. Circa i salari, il comportamento è pressoché identico.
L'unica differenza sensibile è che coi dati di Wolff nel 1947 i due indici tornano a coincidere, mentre nei miei dati rimangono scostati, ma la caratteristica più rilevante, cioè lo stacco della produttività a partire dagli anni '70, rimane il medesimo.
Che succede, però, se rappresentiamo le serie prendendone i logaritmi naturali?
Succede questo:
Viste così, le dinamiche che stiamo vivendo, pur restando esplosive, sembrano un po' meno inusuali.
Intanto, una stagnazione del salari si era già avuta a partire dal 1920, ed era durata sostanzialmente fino allo scoppio della Seconda guerra mondiale. In questo periodo, l'indice della produttività ha staccato quello dei salari fino a un massimo di circa il 60%, corrispondente a un po' più di una "tacca" sull'asse delle ordinate (nel 1935). Dopo la guerra i due indici sono cresciuti in parallelo (ma i salari sono rimasti un po' sotto, questo si vede sia nel grafico di Wolff che nel mio). La produttività ha preso di nuovo il "fugone" all'inizio degli anni '80, e da allora l'ulteriore stacco rispetto all'indice dei salari reali è stato di circa il 90% (corrispondente a un po' meno di due tacche sull'asse delle ordinate).
Certo, le dimensioni del fenomeno sono molto maggiori, questo è palese. D'altra parte, oggi il capitalismo non può sfogare le sue tensioni, come ai bei (per lui) tempi andati, scatenando qualche simpatica guerra mondiale, e poi la finanziarizzazione dell'economia è progredita, e anche il keynesismo ci ha messo del suo. La politica fiscale espansiva (di Reagan o di Craxi, con segno, colore e intenzioni diverse) ha messo una bella toppa al cuneo fra salari e produttività negli anni '80, portando a una discreta crescita del debito pubblico negli Stati Uniti e in Italia. Una cosa simili, in fondo, era successa anche negli anni '20, come fa vedere il grafico di Belen e Sbrancia (vedi sopra). Poi, dagli anni '90, il testimone è passato all'indebitamento privato, sia negli Stati Uniti che da noi, e siamo andati avanti per un altro quindicennio. Questo anche concorre a spiegare perché gli squilibri distributivi, e quindi finanziari, accumulati, siano questa volta maggiori.
Ma da qui a dire che "this time it is different", mi dispiace, ma ce ne corre. Non è così "different" (in questo, purtroppo, hanno ragione loro), e quindi è piuttosto futile aspettarsi palingenesi, e piuttosto furbesco suggerire imminenti collassi del sistema, semplicemente usando unità di misura opinabili!
La soluzione è a portata di mano!
È anche piuttosto interessante andare a vedere quale sia la soluzione che Wolff propone per risolvere il problema. Dopo aver sacramentato per pagine e pagine contro Keynes, colpevole, a suo avviso, di aver aiutato il capitalismo a tenere insieme i propri cocci, l'amico Wolff giunge alla conclusione, alla proposta. E qual è, questa proposta? La transizione da un sistema "capitalista" (di Stato, cioè keynesiano, o privato, cioè neoclassico) sarebbe assicurata, "a livello microeconomico", dalla sostituzione dei tradizionali consigli di amministrazione con consigli di fabbrica. I lavoratori, diventando amministratori di se stessi, distribuirebbero il surplus (i guadagni di produttività, diciamo così - suscitando le ire dei puristi) in modo meno iniquo: cioè tirerebbero la coperta dalla parte loro (cosa giusta e sacrosanta). Naturalmente, se i lavoratori diventassero "their own board of directors", il tradizionale conflitto fra capitale e lavoro scomparirebbe, e questo sarebbe un passo decisivo verso una ulteriore democratizzazione della società. Tutto scritto qui, leggere per credere.Ora, io, logaritmi a parte, con l'analisi di Wolff, come con quella di certi marZiani "de noantri" (che prima ti dileggiano e poi ce vanno in puzza), mi ritrovo, assolutamente.
La terapia mi lascia un po' perplesso, perché la vedo sottoposta a due ovvie obiezioni:
1) e se ci dicono di no?
2) e i soldi chi ce li mette?
Cioè, come funziona? Ci svegliamo un giorno, andiamo al lavoro, e diciamo agli amministratori: "Scusate, andatevene a casa, che ora decidiamo noi". Loro se ne vanno, e gli azionisti come la prendono? E le banche cosa fanno? Ah, certo, ma nel frattempo avremo fatto lo stesso anche nelle banche. In simultanea. Be', certo... Son quelle cose un po' così, come avere la luna in trigono con Venere, Mercurio in quadratura con Saturno e Giove in opposizione con Marte: opportunità che si presentano (se possibile) una volta nella vita, e che sarebbe in effetti stupido non sfruttare.
Ragazzi, non so come dirvelo: io vorrei tanto credere che sia possibile avere un mondo migliore... Ma se le proposte sono queste, alla fine preferisco rendere meno peggiore quello nel quale sono nato. Mi scuserete, oppure, deponendo linguaggio liturgico e puzza sotto il naso, mi direte dove sbaglio, e io cercherò di capirlo...
Sono i dettagli che fanno la delizia dell'intenditore.
Bene. Da oggi alcuni di voi sono meno beati: hanno appreso cos'è la quota salari, hanno appreso che non volevo nasconder loro nulla, hanno ricordato cosa sono i logaritmi, e si sono deliziati nell'apprendere che anche di essi può esser fatto un uso ideologico. Ogni tecnica rinvia a una metafisica, e sono sempre i dettagli a far la delizia dell'intenditore.Ad esempio, ascoltatevi questo. Ich will den Kreuzstab gerne tragen: porterò con gioia la croce (che viene dalle mani del Signore). Anche se avete le orecchie devastate dalla musica cessica che ascoltate tutto il santo giorno, lo sentite che su Kreuz c'è una nota molto espressiva? Bach usa un intervallo strano, una seconda eccedente (si bemolle-do diesis, non sto parlando di tette ma di note). E anche qui, uno direbbe: "Bello, sì, forse, ma comunque mastica...".
E invece no, perché c'è il dettaglio (che fa la gioia dell'intenditore). Guardate com'è scritto:
Visto? Per aumentare la seconda, rendendola eccedente, Bach mette un diesis, che sarebbe questo segno # (er cancelletto), sul do che corrisponde alla parola Kreuz. Ora, siccome a quei tempi Twitter non c'era, difficilmente Bach avrà voluto creare l'hashtag #kreuz. Il fatto è un altro: il diesis in effetti è una croce. Insomma: Bach usa il segno grafico dell'alterazione per simboleggiare il concetto espresso dal testo, e sicuramente non lo fa per caso. Vi risparmio altri simboli, come il peso della croce, simbolizzato da un vocalizzo di otto battute sulla a di tragen, ecc. Dal che si evince che qualche volta le seghe mentali possono portare a risultati esteticamente appaganti. Un giorno in cui anche a voi, come a me, la croce che vi siete scelti comincerà a pesare un po' sulle spalle, ricordatevi di questo link, e poi ripartite di slancio.
Noi la croce la portiamo, gerne, ma non è detto che sia destinata a noi stessi.
Concludendo
Le conclusioni qui sono due, una moderna, e una antica.La prima è che
La Nature est un temple où des vivants piliers
laissent parfois sortir des confuses paroles ;
l'homme y passe à travers des forêts de symboles
qui l'observent avec des regards familier.
e quindi, in queste circostanze,
...nihil dulcius est, bene quam munita tenere
edita doctrina sapientum templa serena,
despicere unde queas alios passimque videre
errare atque viam palantis quaerere vitae,
certare ingenio, contendere nobilitate,
noctes atque dies niti praestante labore
ad summas emergere opes rerumque potiri.
Con gli ambiziosi madre Natura sarà sempre matrigna, e ai superbi e agli incolti nasconderà i suoi rutilanti colori. Insomma: poveri piddini, non sanno cosa si perdono. E per chi non avesse, da madre Natura, ricevuto il dono incomparabile di leggere fra le righe, suggerisco sommessamente questa chiave di lettura.
(O miseras hominum mentes, o pectora caeca! Eppure Keynes ve l'ha detto che nel lungo periodo sarete tutti morti. Certo, certo, anch'io, si sa. Ma prima, col vostro permesso, voglio seppellirne un bel po'...).














Nessun commento:
Posta un commento
5 STELLE